Baka je napravila veliku tortu kvadratnog oblika za svoje unuke. Kao ukras, uzduž i popreko je stavila šlag preko torte, podelivši je na n x n kvadratnih polja jednake veličine. Na kraju je na svako polje prosula određen broj čokoladnih mrvica.

Baka seče tortu na sledeći način: Prvo odabere jednu od četiri strane torte sa koje će da krene da seče, a zatim odabere između kojih redova, odnosno kolona, će da seče tortu. Posle toga se ne menja ni pravac, ni smer sečenja dok se sečenje ne završi. Ukoliko je ovo prvo sečenje u tom pravcu i smeru, baka seče od ivice torte. Ako je ranije već sekla u tom pravcu i smeru, onda seče od mesta završetka poslednjeg sečenja u tom pravcu i smeru. Nakon što počne da seče parče, ne zaustavlja se do njegove suprotne ivice, odnosno dok ga potpuno ne preseče. Ništa se ne seče ako je torta več presečena celom dužinom u datom pravcu.

Pošto svi njeni unuci mnogo vole čokoladne mrvice, baka ne želi da neko dobije ni premalo, a ni previše mrvica na parčetu.

Vama je dato je q upita jednog od sledeća dva tipa:

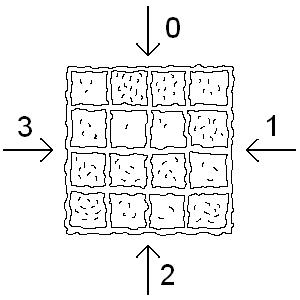
• 1 a b - torta se seče u smeru a (jednom od četiri kao na slici). Ako je horizontalno sečenje, torta se seče između redova b i b + 1. Ako je vertikalno sečenje, torta se seče između kolona b i b + 1.
• 2 l h - potrebno je odgovoriti koliko parčadi trenutno postoji takvih da je broj mrvica na parčetu u intervalu [l, h].

Ulaz:

(Ulazni podaci se učitavaju sa standardnog ulaza) U prvom redu ulaza se nalaze brojevi n i q (1 ≤ n≤ 500, 1 ≤ q ≤ 100.000), dimenzija torte i broj upita. U sledećih nredova nalazi se po n brojeva, broj mrvica na svakom polju torte. Svako polje će imati najmanje jednu, a najviše 2*10⁹ mrvica. Zatim sledi q redova koji predstavljaju već opisane upite formata t i j, gde t ∈ {1,2}. Ako je t = 1, onda 0 ≤ i ≤ 3 i 1 ≤ j ≤ n - 1. Ako je t = 2, onda 1 ≤ i ≤ j ≤ 10¹⁵. Upiti se izvrxavaju u redosledu datom na ulazu.

Izlaz:

(Izlazni podaci se ispisuju na standardni izlaz) Za svaki upit tipa 2 iz ulaza ispisati u novi red izlaza odgovor na taj upit (odgovore ispisivati u odgovarajućem redosledu). Postojaće bar jedan upit tipa 2.

Primer 1:

4 6
3 12 8 5
4 1 2 9
7 6 6 3
10 4 2 8
1 2 1
1 3 3
2 9 15
1 3 3
2 13 14
2 17 100

2
2
1

Objašnjenje.

Za dati primer, sečenja su prikazana na slikama:

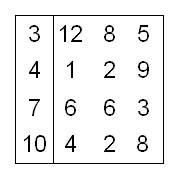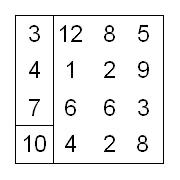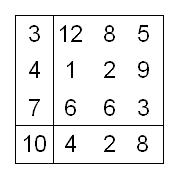Posle 1. sečenja	Posle 2. sečenja	Posle 3. sečenja

Napomena.

• U 20% test primera biće n, q≤ 100.
• U 40% test primera broj upita tipa 1 neće preći 1.000.