Stanovnici jednog malog sela bave se ribarenjem i programiranjem. Nakon završenog ribolova, ribari svoje čamce ostavljaju duž jedne obale uskog kanala. Svaki ribar ima jedan čamac i sopstveni stubić negde duž kanala koji mu služi za privezivanje čamca, pri čemu sme da priveže svoj čamac isključivo za svoj stubić. Čamci moraju biti ostavljeni tako da svaki čamac bude tačno uz svoj stubić, što znači da stubić mora biti negde neposredno pored čamca, tj. između dva kraja čamca (dozvoljeno je i da stubić bude neposredno pored nekog kraja čamca). Pošto je kanal uzan, najviše jedan čamac se može nalaziti na svakom poprečnom preseku kanala, odnosno svi čamci moraju biti privezani neposredno do obale. Čamci se mogu dodirivati svojim krajevima.

Zbog ovakvog vezivanja čamaca nije obavezno moguće da čamci svih ribara budu vezani istovremeno. Zato su ribari zamolili svoje prijatelje programere da im izračunaju koliko najviše čamaca može istovremeno biti vezano. Međutim, programerima je ovo bio pretežak zadatak, pa su i oni počeli da se bave ribarenjem, a zadatak su prepustili vama.

dozvoljena vezivanja		nedozvoljena vezivanja

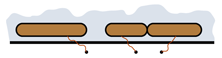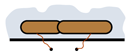
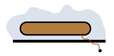Ulaz:

Ulazni podaci se učitavaju sa standardnog ulaza. U prvom redu zapisan je samo broj ribara n (1 ≤ n ≤ 10000). U svakom od narednih n redova zapisani su prirodni brojevi l_i i p_i (1 ≤ l_i, p_i ≤ 100000) razdvojeni jednim razmakom, koji redom označavaju dužinu čamca i položaj (koordinatu) stubića i-tog ribara. Nijedna dva stubića nemaju istu koordinatu.

Izlaz:

Na standardni izlaz treba upisati samo jedan broj - koliko najviše čamaca može biti privezano istovremeno.

Primer:

7
5 9
2 17
6 10 
3 11
2 16
4 13
5 6

5

Objašnjenje:

Najviše je moguće da 5 čamaca bude istovremeno vezano, na primer čamci 1, 2, 4, 5 i 7.