Data su dva prirodna broja n i m. Broj n možemo zapisati u dekadnom zapisu preko niza cifara kao n = c_kc_k-1 ...c₂c₁.

Nad brojem n je moguće primeniti operaciju sečenja između neke dve uzastopne cifre. Ako broj n isečemo na dva dela između cifara i + 1 i i, i ∈ [1, k - 1] dobijamo dva nova broja n₁ = c_k... c_i+1 i n₂ = c_i... c₁. Pri ovom sečenju dozvoljen je i slučaj kada n₂ počinje vodećim nulama, tj. kada je c_i = 0.

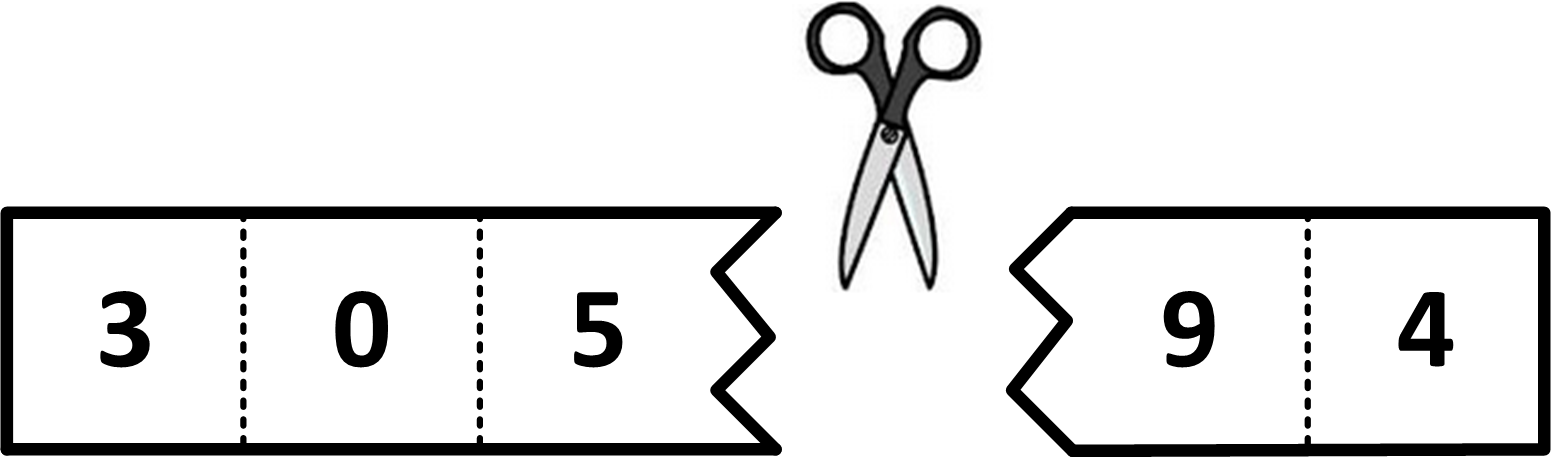
Primer sečenja broja n = 30594 pri čemu se dobija n₁ = 305 i n₂ = 94.

Za date brojeve n i m naći sečenje broja n takvo da je apsolutna razlika sume dobijenih delova, n₁ +n₂ , i broja m minimalna. Drugim rečima, naći sečenje koje minimizira izraz

| m - ( n ₁ + n ₂) |

Ulaz.

(Ulazni podaci se učitavaju sa standardnog ulaza) U prvom i jedinom redu ulazne datoteke nalaze se dva prirodna broja n i m (10 ≤ n , m ≤ 10 ¹⁸) opisana u tekstu problema. Brojevi n i m nemaju vodećih nula.

Izlaz.

(Izlazni podaci se ispisuju na standardni izlaz) U prvom i jedinom redu izlazne datoteke ispisati traženu vrednost (minimalnu apsolutnu razliku broja m i sume delova nekog sečenja broja n).

Primer 1.

30594 400

1

Objašnjenje.

Sva moguća sečenja i odgovarajuće apsolutne razlike za dati primer su:

n1 = 3 i n2 = 0594

197

n1 = 30 i n2 = 594

224

n1 = 305 i n2 = 94

1

n1 = 3059 i n2 = 4

2663