U jednom predgrađu Niša nalazi se velika, takoreći beskonačna njiva u obliku dvodimenzione ravni. Bogata porodica Vatrenić se ne podnosi sa drugom bogatom porodicom Blažić. Porodica Blažić poseduje ~N~ optičkih kablova, ~i~-ti kabl je u obliku beskonačne prave koja prolazi kroz tačke ~(x_i, y_i)~ i ~(u_i, v_i)~. Vatrenići su poznati po paljenju njiva, te je vaš zadatak da za svaki od datih ~Q~ scenarija širenja požara odredite koliko kablova će se oštetiti. Scenario sa rednim brojem ~j~ se odnosi na jedan krug ~K_j~ sa centrom u tački ~(a_j, b_j)~ i radijusom ~r_j~, krug do kojeg će se raširiti požar u tom scenariju. Pritom, za ove krugove važi: ~K_j \subset K_{j+1}~ za svako ~1 \leq j < Q~, drugim rečima, ~j~-ti krug je u potpunosti sadržan u ~(j+1)~-om krugu, takođe, granice nikoja dva kruga se ne dodiruju. Kabl koji je u obliku prave ~p~ će se oštetiti u scenariju ~C~ ako i samo ako je skup ~p \cap C~ neprazan, odnosno, ako se krug i prava seku u bar jednoj tački. Kako je vatra nepredvidiva pojava, u svakom scenariju se garantuje da se rešenje (broj oštećenih kablova) neće promeniti čak ni ako se poluprečnik kruga ~r~ poveća ili smanji za ~r \cdot 10^{-12}~.

Opis ulaza

U prvoj liniji standardnog ulaza nalazi se prirodan broj ~N~ - broj kablova koje poseduje porodica Blažić. U narednih ~N~ linija nalaze se po četiri cela broja, ~x_i, y_i, u_i, v_i~, koordinate dve tačke kroz koje prolazi ~i~-ti kabl. Naredna linija sadrži jedan prirodan broj ~Q~, broj scenarija. U narednih ~Q~ redova nalaze se po tri cela broja ~a_i, b_i, r_i~, koordinate centra kruga i poluprečnik kruga kod ~i~-tog scenarija.

Opis izlaza

Za svaki od ~Q~ scenarija ispisati po jedan ceo broj - u ~j~-ti red ispisati broj kablova koji će se oštetiti u scenariju pod rednim brojem ~j~.

Primer 1

Ulaz

4
4 -3 -5 1
6 -2 -4 10
6 11 6 8
6 8 6 11
3
0 5 1
1 4 3
3 5 6

Izlaz

1
1
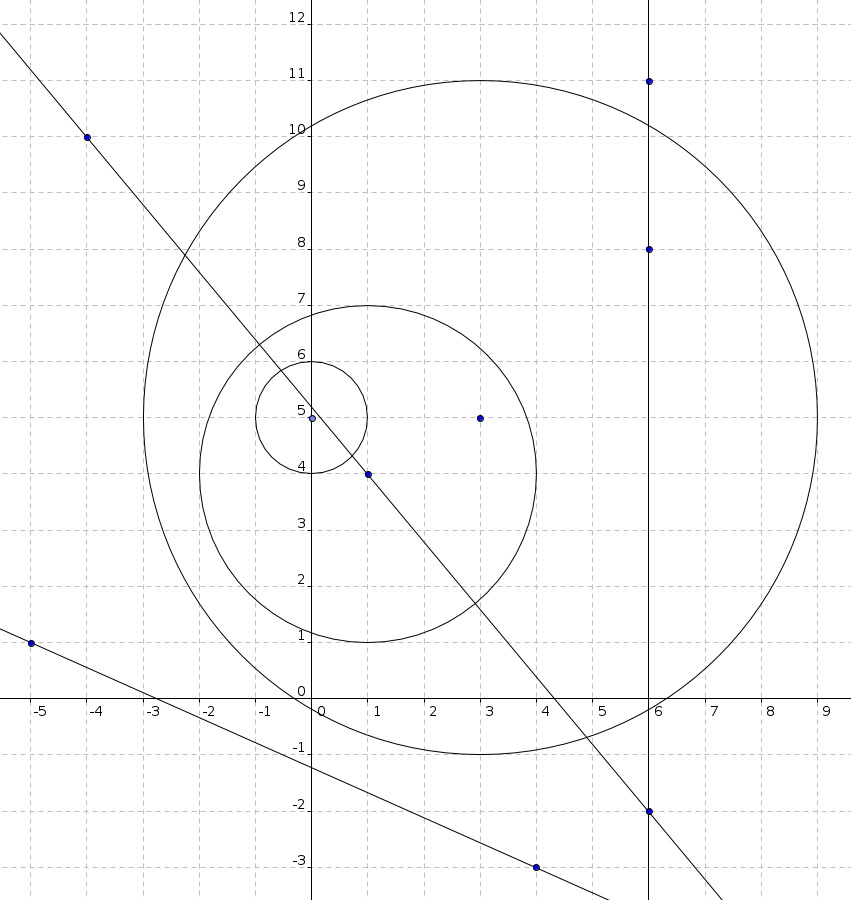
3

Objašnjenje primera

U prva dva scenarija će se oštetiti samo jedan kabl (kabl sa rednim brojem ~2~), dok će se u trećem scenariju pored ovog oštetiti i kablovi sa rednim brojevima ~3, 4~ (koji su podudarni).

Ograničenja

U svim test primerima važi:

• ~-10^8 \leq x_i, y_i, u_i, v_i, a_j, b_j \leq 10^8~ za svako ~1 \leq i \leq N, 1 \leq j \leq Q~
• ~1 \leq r_j \leq 10^8~ za svako ~1 \leq j \leq Q~
• ~N, Q \leq 100000~.
• Za svako ~1 \leq i \leq N~ važi da se tačke ~(x_i, y_i)~ i ~(u_i, v_i)~ ne podudaraju.

Test primeri su podeljeni u sledeće grupe:

• U test primerima vrednim 20 poena: ~N, Q \leq 500~.
• U test primerima vrednim 20 poena: ~a_i = a_j, b_i = b_j~ za svako ~1 \leq i, j \leq Q~.
• U test primerima vrednim 20 poena: ~y_i = v_i~ za svako ~1 \leq i \leq N~.
• U test primerima vrednim 40 poena: Nema dodatnih ograničenja.